順列 \(P\) における操作 \(P_i \to P_{P_i}\) (ABC377-E)
2024-11-20 22:29 +0900 [Last modified : 2024-11-21 00:42 +0900]
問題概要
\( P = (P_1, P_2, ..., P_N) \) について，操作 \( P_i \to P_{P_i} \) を全ての \(i\ (1 \leq i \leq N)\) で同時に \(K\) 回繰り返したあとの \(P\) を求めよ．
\(i\ (1 \leq i \leq N)\) について有向辺 \( i \to P_i \) を張ったグラフを考えたとき，\(i\) から \(2^K\) 回だけ移動した頂点が \(P_i\) となる．
言われてみればそんな気もするが，はっきり理由が理解できていないので記録を残して覚える．
証明
入力例1について，有向辺 \( i \to P_i \) を張ったグラフは次の通り．GRAPH × GRAPHで作成 (monkukui様～～)
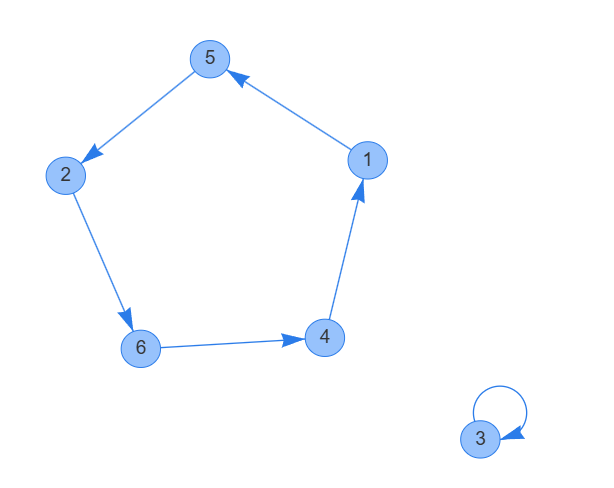
解説に倣い帰納法で考える．
\(K = 0\) のとき
有向辺 \( i \to P_i \) を張っているから，頂点 \(i\) から \(2^0 = 1\) 回だけ移動した先の頂点は \(P_i\) である．
\(K = k\) で成り立つとき
\(P_i\) は頂点 \(i\) から \(2^k\) 回だけ移動した先の頂点である．
もう一度操作を行ったとき (\(K = k+1\)) の \(P_i\) は，現在の \(P_{P_i}\) である． 現在の \(P_{P_i}\) は頂点 \(P_i\) から \(2^k\) 回だけ移動した先の頂点であるから，頂点 \(i\) から \(2^k + 2^k = 2^{k+1}\) 回だけ移動した先の頂点に等しい．
よって，\(K = k+1\) の \(P_i\) は頂点 \(i\) から \(2^{k+1}\) 回だけ移動した先の頂点である．
\( i = 1, K = 3 \) などを例に挙げて考えるとわかりやすそう．
一度このグラフについて考えれば証明はすぐできそう． 有向辺 \( i \to P_i \) を考えること自体がこれ系の問題で典型なのか？